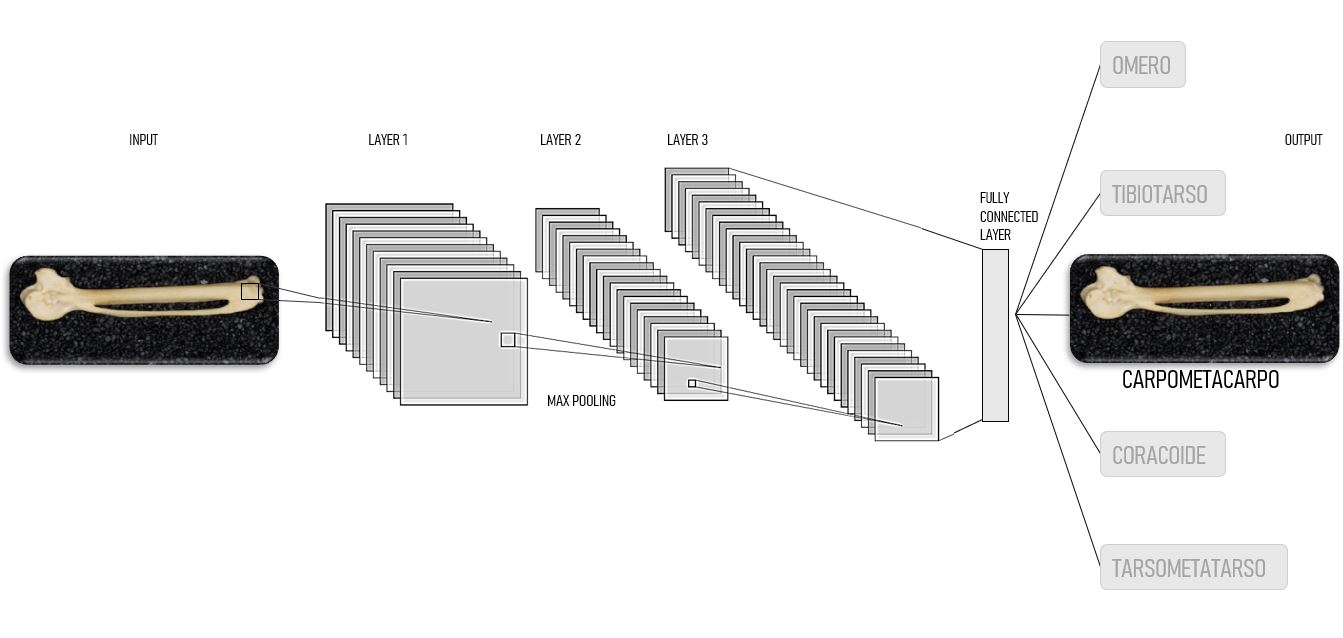
Lo scopo di questo paragrafo è di introdurre il lettore curioso alla costruzione di FIRENET e alla teoria sottostante. Vedi questo articolo.

Come sopra citato, un modello è instabile se esiste una perturbazione piccola in norma che, se sommata all’input, cambia significativamente l’output del modello. Analizzando l’instabilità da un punto di vista teorico, è possibile determinare una condizione necessaria per la stabilità di un modello: la kernel awareness. Intuitivamente, un metodo di ricostruzione di un segnale manca di kernel awareness se raggiunge una prestazione eccessiva nella ricostruzione di due vettori le cui misurazioni sono vicine in norma. In altre parole, la mancanza di kernel awareness può essere vista come l’eccessiva adattabilità di un modello alle misurazioni in input, problema a cui tendono i modelli allenati con la procedura di addestramento tipica del deep learning.

La teoria del Compressed Sensing per trovare alcune ipotesi sull’operatore di sub-sampling A che garantiscono la kernel awareness del modello di ricostruzione. Il Compressed Sensing è un campo di ricerca che studia la ricostruzione di un segnale da informazioni lineari incomplete supponendo che il segnale abbia una struttura di sparsità. Inoltre, al fine di evitare una procedura di addestramento, la rete neurale è stata costruita tramite una tecnica di unrolling dell’algoritmo di ottimizzazione Primal-Dual descritto in [1] e applicato al problema di ottimizzazione.

Presentiamo ora i risultati numerici dell’analisi sperimentale, che confermano matematicamente le impressioni visive descritte sopra. Questo confronto tra le performance di FIRENET e dell’interpolazione bicubica viene mostrato attraverso due metriche: il Root mean squared error (RMSE) e il peak signal-to-noise ratio (PSNR), definito da
PSNR(x,z) = 20 \log_{10} \frac{max(x,z)}{RMSE(x,z)}.
dove x è l’immagine originale, z è l’immagine ripristinata e max(x, z) è il valore massimo tra i pixel di x e z. Inoltre, per misurare la magnitudine del rumore rispetto all’immagine, abbiamo utilizzato la metrica Noise Over Measurement (NOM), che è semplicemente la norma dell’errore fratto la norma dell’input y.

Infine, abbiamo ripetuto la ricostruzione utilizzando due diverse immagini ad alta risoluzione, al fine di mostrare che le prestazioni ottenute sull’immagine PEPPER non sono limitate a questo singolo caso.